n次ベジェを描けるようになろう

2019年8月14日プログラミング

※この記事は前のブログで2018年12月17日に投稿されたものです。最新の情報ではない可能性があります

こんにちは。最近ジーンズの膝の部分に穴が空いてダメージジーンズになった水珈琲です。
この記事はアドベントカレンダーに参加してるそうです。

突然ですが、みなさんはベジェ曲線を知ってますか？canvasなんかで使った事がある人も多いと思います。
しかし、大半のソフトウェアでは2次ベジェ、3次ベジェのみに対応しており、n次ベジェ（nは4以上の自然数）に対応していないことが多いです。

この記事では、ベジェ曲線の仕組みを知り、自分で描けるようになるのを目標にしています。

n次ベジェのイメージを掴みたい方はこちらで遊んでみてください。

Sponsored Links

第一章 ベジェ曲線って何？

この章では、ベジェ曲線のうっすら概要を説明します。

簡単に言うとベジェ曲線というのはコンピュータで扱いやすい曲線の描画方法です。

Wikipediaでは

ベジエ曲線とは、N 個の制御点から得られる N − 1 次曲線である。「ベジェ曲線」『ウィキペディア日本語版』　2018年2月3日(土)01:00　UTC

と表現されています。

よくわからない人も多いと思うので、私なりの言葉にすると、「めっちゃ短い直線をくねくね繋げたら曲線に見える気がする」です。更に意味不明になったと思うのでgif画像を見てもらいたいと思います。下記画像は所謂2次ベジェ曲線です。


実際にn次ベジェが試せるページ

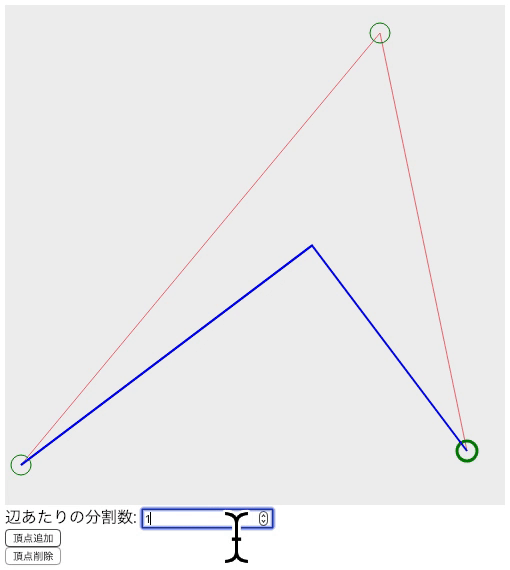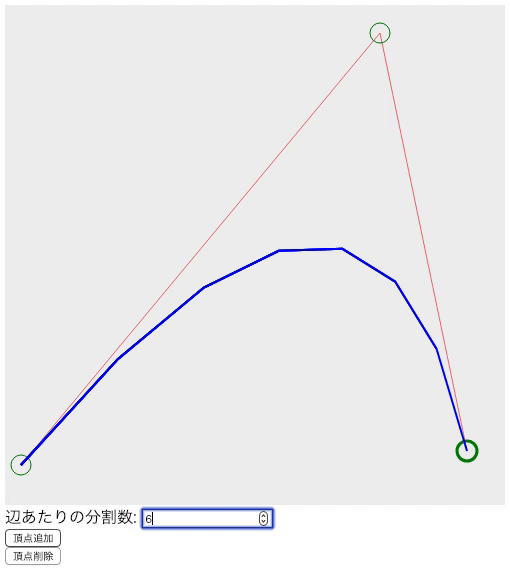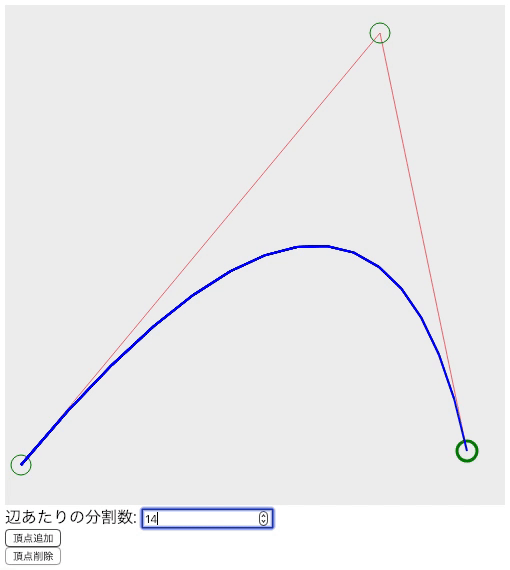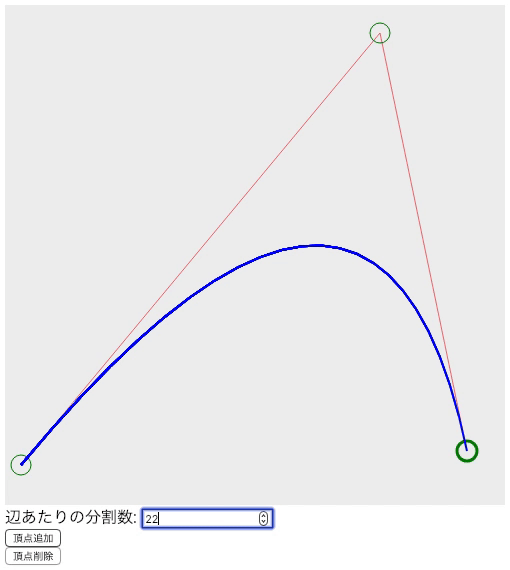
上の画像を見ると２０辺りから直線感は無くなっていると思います。
この章では、ベジェ曲線っていうのは直線の集合なんだな〜というのが分かってもらえたら十分です。

第二章 ベジェ曲線を描こう

この章では、実際にベジェ曲線を（出来れば皆さんの手で）書いてみたいと思います。

2次ベジェ曲線

まず、2次ベジェ曲線は

前提条件: 0 < n < 1

  1. 各辺の長さ*n の場所同士を直線で結ぶ
  2. 結んだ直線の長さ*n の場所にマークを打つ
  3. 滑らかになるまで1と2を繰り返した後、それらのマークを直線で繋げる

という手順で描くことができます。
nの分割を細かくするとするほど滑らかになります。

今回は、手書きがしやすいので4分割（分割点は3つ）にしたいと思います。
分割点は、0.25・0.5・0.75になります。分かりやすいので、0.5（=中心）から始めます。

下準備

まず、「制御点」というものを配置します。今回は2次ベジェ曲線なので、3個の制御点が必要です。

そして、それらを直線で繋ぎます。

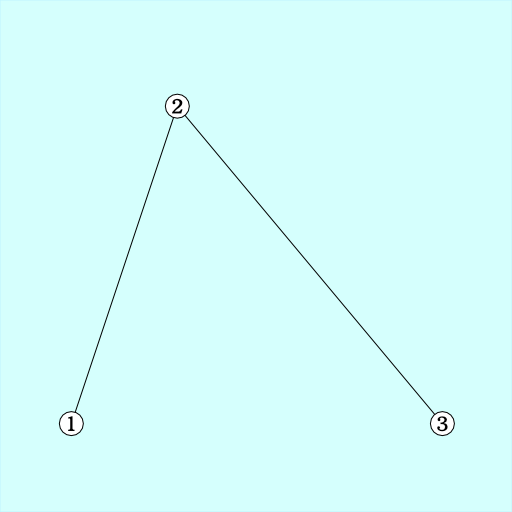
n = 0.5

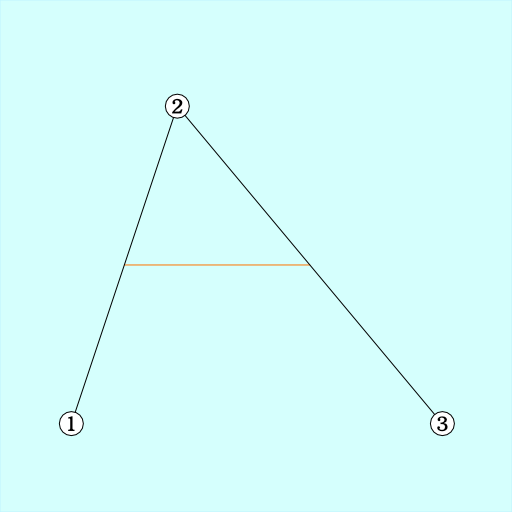
手順1. 各辺の長さ*n の場所同士を直線で結ぶ

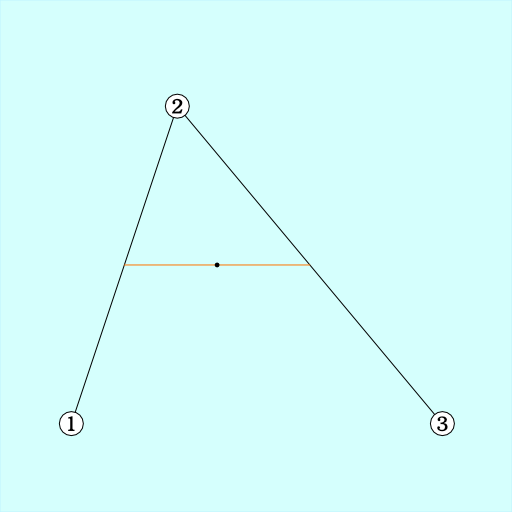
手順2. 結んだ直線の長さ*n の場所にマークを打つ

n = 0.25

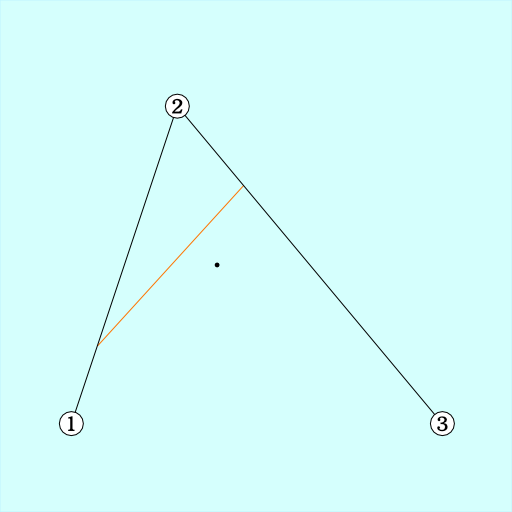
手順1. 各辺の長さ*n の場所同士を直線で結ぶ

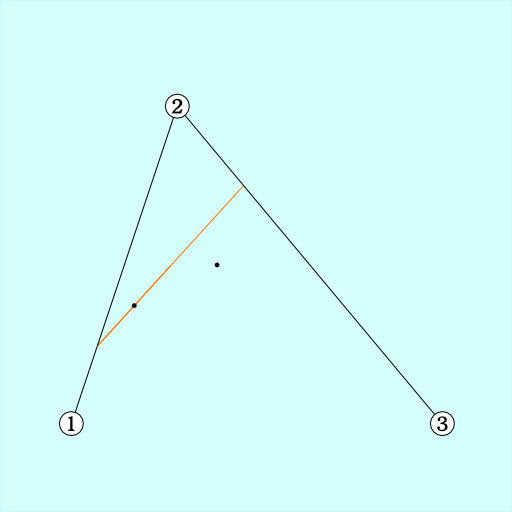
手順2. 結んだ直線の長さ*n の場所にマークを打つ

n = 0.75

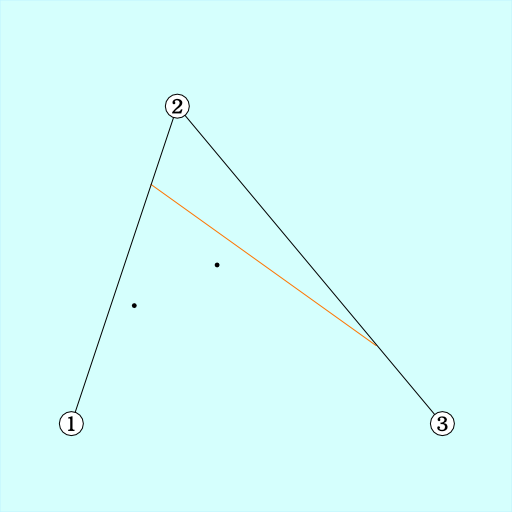
手順1. 各辺の長さ*n の場所同士を直線で結ぶ

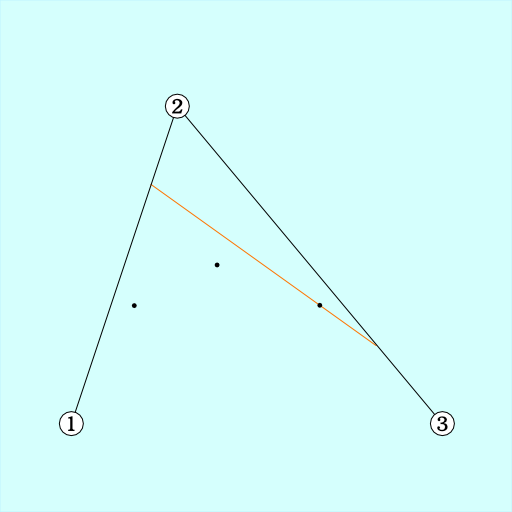
手順2. 結んだ直線の長さ*n の場所にマークを打つ

仕上げ

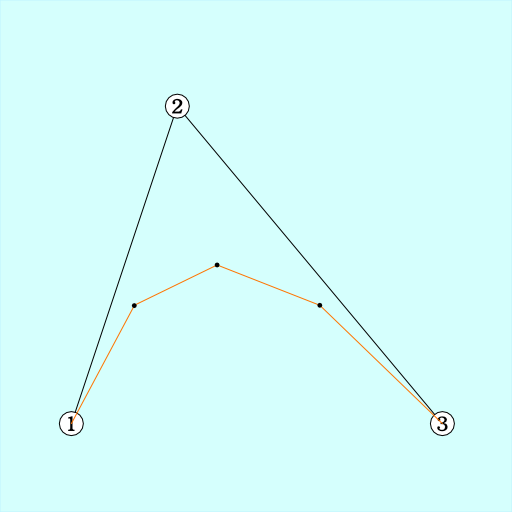
手順3. 滑らかになるまで1と2を繰り返した後、それらのマークを直線で繋げる

これが曲線？と思う人も多いと思いますが、定義的にはベジェ曲線（と呼んで大丈夫なはず）です。上のサンプルは4分割ですが、例えば8分割にすれば

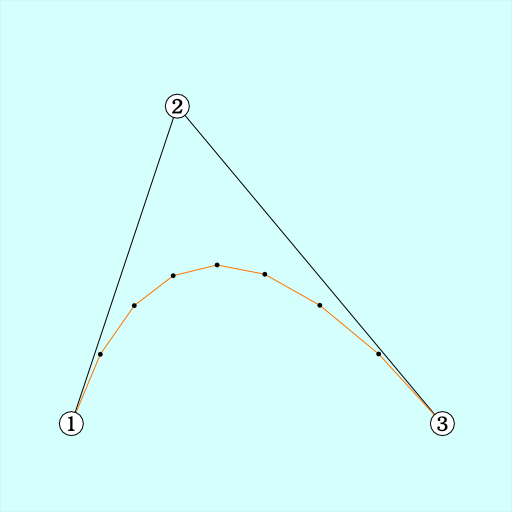
結構曲線っぽくなります。

n(>=3)次ベジェ曲線

n(>=3)次以降のベジェ曲線は、2次ベジェ曲線の描き方+αで描くことができます。

3次ベジェ曲線は、

前提条件: 0 < n < 1

  1. 各辺の長さ*n の場所同士を直線で結ぶ
  2. もし、その直線が複数ある（折れている）場合、その線に対して上の処理をする
  3. 結んだ直線の長さ*n の場所にマークを打つ
  4. 滑らかになるまで1と2を繰り返した後、それらのマークを直線で繋げる

となります。

また同じように手順を追うと大変なので、1つだけサンプルを置いておきます。

n = 0.25

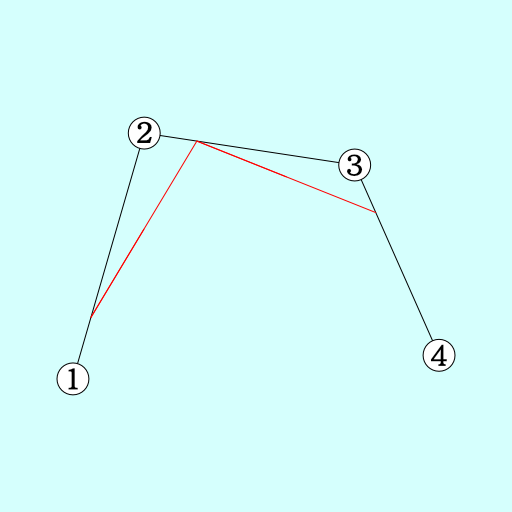
手順1. 各辺の長さ*n の場所同士を直線で結ぶ

手順2. もし、その直線が複数ある（折れている）場合、その線に対して上の処理をする

該当するので、手順1に戻ります（続きの内容は下です）

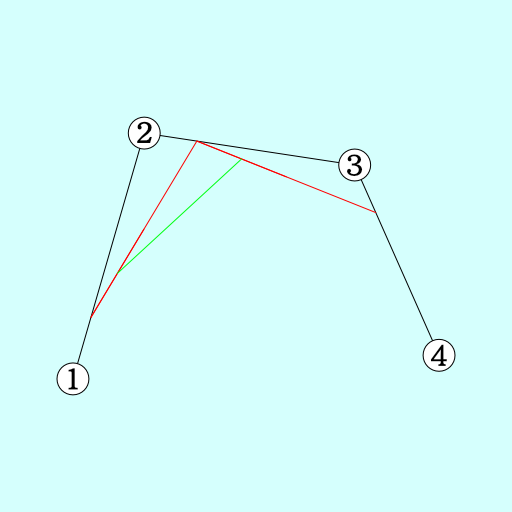
手順1. 各辺の長さ*n の場所同士を直線で結ぶ

手順2. もし、その直線が複数ある（折れている）場合、その線に対して上の処理をする

今度は該当しないので、手順3に進みます。

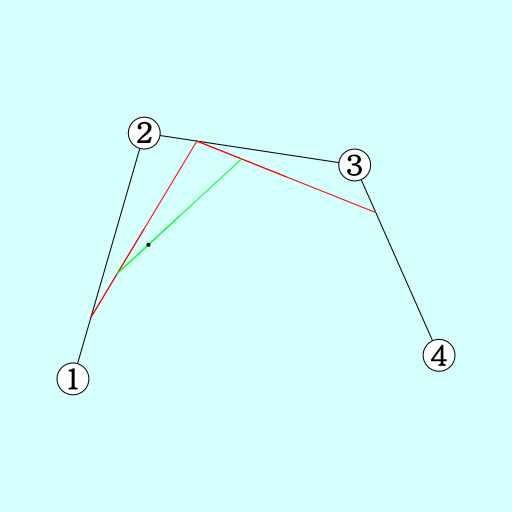
手順3. 結んだ直線の長さ*n の場所にマークを打つ

この処理を、繰り返せばn(>=3)次以降のベジェ曲線も描く事ができます！

第三章 プログラムに起こそう

サンプルソース

module.exports = (points, fineness) => {
  if (points.length < 3) return []
  if (fineness <= 0) return []
  if (points.some(p => p.length < 2 || !Number.isFinite(p[0]) || !Number.isFinite(p[1]))) return []
  let lines = []
  for (let i = 0; i < points.length - 1; i++) lines.push(lineSplit(points[i][0], points[i][1], points[i + 1][0], points[i + 1][1], fineness))
  const bezier = [];
  bezier.push([points[0][0], points[0][1]]);
  [...Array(fineness)].forEach((n, index) => {
    let l = lines.map(e => e[index])
    while (l.length > 1) {
      let t = []
      for (let i = 0; i < l.length - 1; i++) {
        t.push(lineSplit(l[i][0], l[i][1], l[i + 1][0], l[i + 1][1], fineness)[index])
      }
      l = t.slice()
    }
    bezier.push([l[0][0], l[0][1]])
  })
  bezier.push([points[points.length - 1][0], points[points.length - 1][1]])
  return bezier
}
const lineSplit = (x1, y1, x2, y2, split) => [...Array(split)].map((e, i) => ([x1 + ((x2 - x1) / (split + 1)) * (i + 1), y1 + ((y2 - y1) / (split + 1)) * (i + 1)]))

pointsが[ [x,y], [x,y] … ]という形式の制御点の配列、finenessが分割数です。

本当は説明を付けたかったのですが、時間と体力の都合上省かせていただきます…すみません…
ソースを読んで解読してみてください…分からない部分はコメントで質問してください！

このプログラムは、あくまでも制御点の配列から直線の配列に変換するだけなので、基本的にプログラムを移植してしまえばx,yを指定して直線を描画できる環境であればどこでもn次ベジェ曲線を描くことができます！

まとめ

駆け足で解説してみましたが、分かりましたでしょうか…
ベジェ曲線が描けると、表現の幅が少しですが広がります。いざ描いてみるとそれほど難しいものでもないので、是非プログラムに取り入れてみてください！

プログラミング4次ベジェ曲線, ベジェ曲線

Posted by mizucoffee